Torneio de Xadrez a nível de escola a realizar ainda no segundo período. Inscrições na Mediateca e na Ciberteca até 18 de Fevereiro.

Pavilhão do Conhecimento

-Chama-se L. Antunes, frequenta o 12º ano na D. João II e venceu um torneio de xadrez a nível concelhio tendo vencido todas as partidas disputadas.Parabéns!

-“Quem devia fazer exames eram os professores de Matemática e de Português que não percebem nada disto e são responsáveis pelo estado a que isto chegou!”. Joana, 9ºano

-O Tomás tem 11 anos e anda no 6ºano. É colega de turma do meu filho e enganou-se na página do TPC do livro de exercícios. O suposto trabalho de casa dizia respeito a matéria ainda não leccionada. Apesar de não perceber nada do que era pedido não desistiu, consultou o manual e resolveu todos os exercícios relativos à divisão de fracções. A caminho da escola contou-me o sucedido e explicou com clareza como é que se dividem fracções (generalização).
Tomara eu que a terça parte dos meus alunos do décimo ano tivesse tais conhecimentos. Nem me atrevo a fazer a experiência. Já agora, que para aqui convoquei a experiência, devo referir que estou convicto que quem não quer de facto aprender, não aprende e nada há a fazer. Em alguns dos meus alunos do secundário falta quase tudo desde capacidade de trabalho a aspectos cognitivos. Creio que os encarregados de educação não de apercebem da extensão das lacunas, pois alguns referem que os seus filhos até eram muito bons a Matemática no 7º, 8º e 9º. Os pais devem ter consciência que tirar notas elevadas e ser muito bom nem sempre é a mesma coisa. Em turmas muito fracas pode ocorrer uma excessiva sobrevalorização de alunos médios ou menos fracos.
Implicitamente é o professor que é posto em causa (“...ele até era bom...”) por uns e acusado por outros na questão da sobrevalorização.

-O sinistro campo de morte e horror, Auschwitz, ainda assusta. Eminentes e serviçais programadores afugentaram para lá da meia-noite um documentário que devia ser visto, falado e reflectido em família num horário (dito) nobre. Continua a interessar manter as novas gerações na ignorância e futilidade. Tudo tem a ver com tudo!

Pavilhão do Conhecimento - Lisboa

A situação partiu de dois alunos do nono ano.
O Daniel dizia que era possível calcular a área de um quadrado do qual se conhecia apenas a medida da diagonal, o seu colega de carteira não concordava alegando que a insuficiência de dados tornava o problema insolúvel.

O Daniel apresentou, então, uma demonstração, simples mas elegante, que sustentava a sua afirmação. Partiu de um quadrado [ABCD] cuja diagonal media 2cm. A partir dessa diagonal construiu um segundo quadrado [EFBA] de área 4cm2 e estabeleceu uma relação entre as áreas dos dois quadrados, por um simples processo de decomposição, concluindo que a área do quadrado vermelho é 2cm2, porque é metade da área do quadrado auxiliar.
O aluno referiu que aprendera este processo com o pai, o qual parece apreciar os desafios matemáticos, apesar de estar profissionalmente longe da matemática e das ciências em geral e de não possuir habilitações académicas ao nível do superior. Não posso deixar de aproveitar a oportunidade para felicitá-los pelo trabalho matemático em comum, um exemplo raro e altamente meritório. O jovem fez um brilharete.
E já agora ficam aqui dois desafios para ti, Daniel, para a Sara, e para quem quiser na turma.
1. Preparem um artigo sobre a experiência de Eratóstenes para publicar no blogue do Centro de Recursos.
2. “Professor não existem mulheres matemáticas?” (Sara) Proponho-lhes um pequeno trabalho sobre este assunto.
Estes assuntos surgiram após um exposição sobre a irracionalidade da raiz quadrada de dois.

Tens curiosidade em conhecer o Arafaco?
Já ouviste falar no Santanami?E no Pinanami?
Clica aqui.

- Sim, há uma promiscuidade social que se deve à falta de autonomia individual. O salazarismo infantilizou-nos, fez-nos viver num mundo fictício e sugou-nos todas as forças. Eu não quero culpar o salazarismo por tudo, mas a verdade é que foram 48 anos de não inscrição, de não acontecimento. E herdámos isso. Ainda não recuperámos. O ambiente em que vivemos não nos permite ter intensidade de vida, de pensamento, de acção, para que possamos inscrever-nos na nossa própria vida, na Europa, no mundo global, etc. Uma vez assisti a uma entrevista com o jovem físico português, João Magueijo, que vive em Inglaterra. A repórter perguntava-lhe: "Você trabalha com matemática, não em laboratórios. Não podia ter descoberto essas teorias em Portugal?" E ele respondeu imediatamente: "De maneira nenhuma. Sabe porquê? Por causa da intensidade das trocas de pensamento em que eu vivo quotidianamente. É isso que me faz pensar."

Excerto da entrevisda concedida ao Público pelo filósofo José Gil

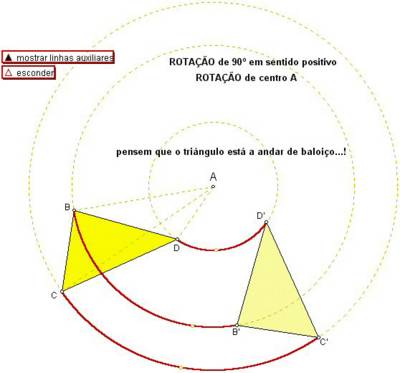
Considera o triângulo [EFG]. Seja A o centro da circunferência dividida em 18 partes iguais.

a) Desenha a imagem do triângulo na rotação de centro A e amplitude 60º em sentido negativo.
b) Desenha o simétrico de [EFG] em relação ao ponto A.
c) Indica a amplitude de DAB (vértice A)e de BCD (vértice C) .
d) Supõe que a medida do comprimento do arco BF é 6cm. Determina, com aproximação às décimas, a medida do comprimento da maior corda da circunferência.
e) Determina a área de um quadrado cujos vértices são pontos da circunferência.

Acaso
Incerteza
Aleatório
Estimativas
Amostras
MARGENS DE ERRO - um blogue sobre sondagens e opinião pública.

O exemplo não é uma forma de ensinar, é a única forma de ensinar.
Albert Einstein

O ponto (2,4) pertence ao gráfico de uma função f.
Dos pontos que se seguem, qual não poderá, à partida, fazer parte desse mesmo gráfico? Porquê?
A(-2,4) B(4,2) C(2,-4) D(5,7)

Quadriláteros num barco - Estuário do Sado

TITÃ

Sounds of an alien world-Audio data collected by the Huygens Atmospheric Structure Instrument (HASI), which includes an acoustic sensor, during Huygens' descent, 14 January 2005.

New images from Titan

Titã - Imagens de Um Mundo Novo a 1300 Milhões de Quilómetros da Terra -Público-

Árvores nº5 -Outubro chuvoso-

(continuação)
Se invertermos a ordem, referindo primeiro que uma certa curva não representa uma função porque tem diversos pontos em comum com uma recta vertical, poucos alunos vão perceber a razão de uma segunda explicação com base na definição de Função. Vão certamente considerar que o professor está a complicar...Caso, pura e simplesmente, um professor/explicador/formador/..., justifique que uma curva não representa uma função com base na afirmação -“Não, porque a recta corta o gráfico em dois pontos.”- está, deliberadamente (fraude) ou não (ignorância), a descer a um nível matematicamente pobre. Tal contribui para uma visão fria, acéfala e totalmente desinteressante forma de trabalhar em Matemática.

A compreensão e interiorização de um conceito por parte de um aluno constitui o objectivo maior de um professor numa exposição teórica-conceptual. Para que o processo de apropriação de uma ideia ou de um conceito seja, atendendo ao público alvo, o mais abrangente possível deve existir um leque variado de estímulos diversificados que auxiliem a compreensão do que está em jogo. Num exercício de equilíbrio, procura-se não ceder a facilitismos estéreis nem cair num contraproducente e desmobilizador rigor formalista.
Escreve este texto tendo como pano de fundo o conceito de FUNÇÃO dado e explorado na aula de hoje (décimo ano) na qual apenas visei a definição e questões de linguagem subjacentes.
Na figura está representada uma curva (parábola) que não é a representação gráfica de uma função.

Inevitavelmente PORQUÊ? A resposta alicerça-se na definição de Função. Existe, pelo menos, um valor de x ao qual corresponde mais do que um elemento de y, facto que contraria a definição de Função. Podemos avançar com um exemplo: (0,2) e (0,-2). Caso esta correspondência fosse função o objecto zero não poderia ter duas (ou mais) imagens distintas.
Uma vez abordado e explorado o conceito, o próprio aluno pode concluir que rectas verticais que intersectem uma curva em mais do que um ponto isso significa que a mesma não pode representar uma função. A uma eventual questão sobre este assunto é bom esclarecer que não é aceite a resposta: "Não, porque a recta corta o gráfico em dois pontos." Não será aceite porque é fundamental que se entenda o motivo pelo qual isso não pode ocorrer!

150000 mil vítimas dão direito a três minutos de silêncio -seis (3 às 11 e 3 às 12) em Portugal por causa da diferença horária e por via das dúvidas...-. Para homenagearmos, em coerência, as vítimas dos flagelos em África precisaríamos de cinquenta minutos de silêncio. É da mais elementar proporcionalidade.
Um campeão alemão de F1, bom rapaz, fez um avultado donativo com direito a notícia de relevo nos noticiários. Será que oferece dezasseis vezes esse montante para as famílias dos 2500000 mortos/ano africanos ou será desaconselhado pelos seus conselheiros para assuntos fiscais?
O que difere nestas duas realidades trágicas é o impacto com que a notícia nos entrou em casa. Não nos devemos esquecer de outras realidades escondidas, igualmente dramáticas e plenas de dor, só pelo facto de não aparecerem nos principais noticiários televisivos.
O empolamento e a exploração até ao limite desta situação secundariza, entre outros aspectos, as trapalhadas da constituição das listas às próximas eleições...

Um projéctil é lançado verticalmente de baixo para cima. Admite que a sua altitude h (em metros), t segundos após ter sido lançado, é dada pela expressão

h(t)=100t-5t^2

i) Determina h(2).
ii) Resolve a equação h(t)=0
iii) Qual o significado dos valores obtidos anteriormente no contexto apresentado?
iv) (para alunos do 12ºano) Qual a velocidade do projéctil, dois segundos após o lançamento?

Estes dois primeiros dias de aulas tiveram, pelo menos, uma regularidade. Ontem e hoje vários alunos de diferentes anos lectivos, procuraram endereços de sites sobre o tsunami no Índico.

Deixo aqui um link para um blogue francês no qual, por sua vez, se encontram bastantes links relativos à referida castástrofe.

Para reflexão aqui fica uma questão...

Cette mobilisation immesurable face à ce cataclysme monstrueux, n’est pas très logique : Cette année (2004) 2,5 millions d’africains sont décédés … suite aux maladies (SIDA, palu) ou aux conflits religieux ou rebelles… Alors pourquoi cette inégalité ?

Árvores -nº4 - ESE Setúbal-

Congratulo-me pela decisão de elogiar publicamente, na página da escola, alunos da D.João II que se destacam pelos trabalhos realizados ou pelo sucesso que alcançam, como é o caso do promissor atleta de natação -recordista nacional absoluto e participante nas Olímpiadas de Atenas- TIAGO VENÂNCIO.

PLOTEUS
O portal sobre oportunidades de aprendizagem no espaço europeu