Bibliografia:
Veloso, E. ; Viana, JP (1998) – Desafios 6. Porto: Ed. Afrontamento
Veloso, E. (1998) –Geometria temas actuais. Lisboa: IIE
Enzensberger, HM (1998)– O Diabo dos Números. Lisboa: Ed. ASA
Struik, DJ (1989) – História Concisa das Matemáticas. Lisboa: Gradiva
Visitem a Mediateca...
outubro 31, 2004
outubro 29, 2004
JACINTO JOÃO
Fotografia de Arl.
Morreu um criativo!
Meio desengonçado de pernas tortas, deixava os defesas sentados e de olhos vesgos. Nas tardes de génio era impossível desarmá-lo sem recorrer a métodos ilícitos. Em Inglaterra chegaram a interromper um jogo para que pudesse ser aplaudido...pelo público da equipa adversária. O gozo supremo da finta. Acho mesmo que devia preferir voltar atrás e fintar de novo o pobre defesa, em lugar de prosseguir para a linha de fundo e centrar para o golo do Guerreiro, do Arcanjo, do Vítor Baptista, do Torres, do Câmpora, do Duda, ...
Hoje morreu o JJ!
Morreu um criativo!
Meio desengonçado de pernas tortas, deixava os defesas sentados e de olhos vesgos. Nas tardes de génio era impossível desarmá-lo sem recorrer a métodos ilícitos. Em Inglaterra chegaram a interromper um jogo para que pudesse ser aplaudido...pelo público da equipa adversária. O gozo supremo da finta. Acho mesmo que devia preferir voltar atrás e fintar de novo o pobre defesa, em lugar de prosseguir para a linha de fundo e centrar para o golo do Guerreiro, do Arcanjo, do Vítor Baptista, do Torres, do Câmpora, do Duda, ...
Hoje morreu o JJ!
outubro 28, 2004
MUDANÇA em perspectiva em virtude de alterações climáticas.

Imagem obtida no site do jornal francês LE MONDE
outubro 25, 2004
POLIEDROS
Sólidos Platónicos
Sólidos Arquimedianos
Download grátis de uma versão de avaliação - POLY-

Sólidos Platónicos
Sólidos Arquimedianos
Download grátis de uma versão de avaliação - POLY-
Escolham um dos sólidos acima referidos.
Construam esse sólido geométrico -cartolina, polidrons,...- e apresentem-no na aula do dia 2 de Novembro, incluindo nessa apresentação algumas das suas características e propriedades.
outubro 24, 2004
MEGACIÊNCIA
-acções espectaculares
-curiosidades
-ciência e cozinha
"Engarrafar uma nuvem não é magia. Com um pouco de ciência, já é possível ter um pedaço de céu guardado numa garrafa!"
Um programa na SIC, aos domingos ao início da tarde...
-acções espectaculares
-curiosidades
-ciência e cozinha
"Engarrafar uma nuvem não é magia. Com um pouco de ciência, já é possível ter um pedaço de céu guardado numa garrafa!"
Um programa na SIC, aos domingos ao início da tarde...
outubro 22, 2004
Um quadrado, desenhado num referencial cartesiano, tem cada um dos vértices num quadrante diferente.
São conhecidas as coordenadas de dois vértices do quadrado: (-3,3) e (5,-1).
- Determina um valor aproximado às décimas da área desse quadrado.
- Indica as coordenadas do simétrico de (5,-1) em relação a Ox
- Indica as coordenadas do simétrico de (5,-1) em relação a Oy
- Indica as coordenadas do simétrico de (5,-1) em relação à origem do referencial
Segundo o jornal PÚBLICO
Especialistas e ambientalistas portugueses saudaram a ratificação do Protocolo de Quioto pela câmara baixa do Parlamento da Rússia, abrindo caminho à entrada em vigor do acordo internacional que visa reduzir as emissões poluentes responsáveis pelas alterações climáticas.
outubro 20, 2004
outubro 19, 2004
Mais uma vez a questão das prioridades.
Segundo uma professora de Português, o novo programa do décimo ano incentiva particularmente à leitura. Consequentemente, ao que me parece, foram definidas a nível de Departamento várias obras que os alunos terão de ler e efectuar o respectivo guião de leitura.
Os livros são caros? Uns mais que outros!
São mais uma despesa para os pais? É evidente.
E os bares na Luísa Todi também levam uns trocos aos pais e os filmezecos dos SpiderMan e afins também não são à borla!
Segundo uma professora de Português, o novo programa do décimo ano incentiva particularmente à leitura. Consequentemente, ao que me parece, foram definidas a nível de Departamento várias obras que os alunos terão de ler e efectuar o respectivo guião de leitura.
Os livros são caros? Uns mais que outros!
São mais uma despesa para os pais? É evidente.
E os bares na Luísa Todi também levam uns trocos aos pais e os filmezecos dos SpiderMan e afins também não são à borla!
E os polifónicos com ( e sem...) câmara incorporada...são baratos?!
Quanto é que cada alunos gasta em chamadas dos seus telemóveis? Todas as chamadas efectuadas são impreterivelmente necessárias?
Este assunto pode ser visto e interrogado na perspectiva do que é realmente essencial em contraponto com o acessório e o supérfluo.
Em que é que ficamos?
Da nossa parte, professores, entendemos que a questão deve ser levantada e reflectida. Se nos é permitido, sugerimos que o aspecto financeiro deva ser gerido em função das necessidades de aprendizagem dos jovens e que, de acordo com este pressuposto, as despesas menos importantes sejam secundarizadas relativamente aos livros, ás calculadoras gráficas (caso sejam de aquisição obrigatória) e aos restantes materiais didácticos imprescindíveis nas diferentes disciplinas.
Quanto é que cada alunos gasta em chamadas dos seus telemóveis? Todas as chamadas efectuadas são impreterivelmente necessárias?
Este assunto pode ser visto e interrogado na perspectiva do que é realmente essencial em contraponto com o acessório e o supérfluo.
Em que é que ficamos?
Da nossa parte, professores, entendemos que a questão deve ser levantada e reflectida. Se nos é permitido, sugerimos que o aspecto financeiro deva ser gerido em função das necessidades de aprendizagem dos jovens e que, de acordo com este pressuposto, as despesas menos importantes sejam secundarizadas relativamente aos livros, ás calculadoras gráficas (caso sejam de aquisição obrigatória) e aos restantes materiais didácticos imprescindíveis nas diferentes disciplinas.
Os alunos também se devem consciencializar que a massa não cai do céu e que, por exemplo, algumas prendas de Natal se podem conjugar com as referidas necessidades!
Mais nada!
outubro 18, 2004
outubro 16, 2004
outubro 15, 2004
1. A nova disciplina de Matemática do ensino Secundário – MATEMÁTICA B- permanece envolta em dúvidas que ainda não consegui dissipar.
No segundo período será leccionado o capítulo de FUNÇÕES. A questão que coloco diz respeito à obrigatoriedade do uso de calculadora gráfica –recurso tecnológico obrigatório na Mat. A e no anterior programa cujo código do exame era o 435-. Sendo uma disciplina bianual os alunos deveriam ter, no final do 11ºano, um exame nacional à disciplina. No entanto coloca-se no horizonte uma nebulosa, porque pouco clara, possibilidade de opção, por parte dos alunos, quanto ao exame de formação específica a realizar. Assim, os alunos escolheriam entre Geometria Descritiva e Matemática B. Esta indefinição quanto à questão do exame é determinante para a recomendação da aquisição de uma calculadora gráfica, a qual deve ser feita com alguma antecedência atendendo ao seu considerável custo –no mínimo cerca de 100euros- de modo a acautelar a gestão financeira de cada agregado familiar.
Já nem falo das questões de carácter metodológico inerente à existência de exame nacional...
Remeto este assunto para a instância superior à qual compete a clarificação da situação. As escolas não são responsáveis por regras pouco claras e muitas vezes definidas e alteradas em pleno funcionamento do ano lectivo.
2. Os cursos de S@ber+ - iniciação, consolidação e aprofundamento- estão a chegar a chegar ao fim em virtude do corte de verbas definido pelo Ministério da Educação. O sucesso destes cursos pode ser testemunhado pelos muitos adultos que os frequentaram nas várias áreas –TIC, Matemática para a Vida e Oficinas de Leitura e Escrita -. Estes cursos auxiliaram muitos a ajustar contas antigas consigo próprios, fruto de decisões erradas quando jovens e com o destino que os empurrou prematuramente para o mundo do trabalho, afastando-os cedo demais da escola.
Em Dezembro acabam! Lamentavelmente.
Triste país...
No segundo período será leccionado o capítulo de FUNÇÕES. A questão que coloco diz respeito à obrigatoriedade do uso de calculadora gráfica –recurso tecnológico obrigatório na Mat. A e no anterior programa cujo código do exame era o 435-. Sendo uma disciplina bianual os alunos deveriam ter, no final do 11ºano, um exame nacional à disciplina. No entanto coloca-se no horizonte uma nebulosa, porque pouco clara, possibilidade de opção, por parte dos alunos, quanto ao exame de formação específica a realizar. Assim, os alunos escolheriam entre Geometria Descritiva e Matemática B. Esta indefinição quanto à questão do exame é determinante para a recomendação da aquisição de uma calculadora gráfica, a qual deve ser feita com alguma antecedência atendendo ao seu considerável custo –no mínimo cerca de 100euros- de modo a acautelar a gestão financeira de cada agregado familiar.
Já nem falo das questões de carácter metodológico inerente à existência de exame nacional...
Remeto este assunto para a instância superior à qual compete a clarificação da situação. As escolas não são responsáveis por regras pouco claras e muitas vezes definidas e alteradas em pleno funcionamento do ano lectivo.
2. Os cursos de S@ber+ - iniciação, consolidação e aprofundamento- estão a chegar a chegar ao fim em virtude do corte de verbas definido pelo Ministério da Educação. O sucesso destes cursos pode ser testemunhado pelos muitos adultos que os frequentaram nas várias áreas –TIC, Matemática para a Vida e Oficinas de Leitura e Escrita -. Estes cursos auxiliaram muitos a ajustar contas antigas consigo próprios, fruto de decisões erradas quando jovens e com o destino que os empurrou prematuramente para o mundo do trabalho, afastando-os cedo demais da escola.
Em Dezembro acabam! Lamentavelmente.
Triste país...
outubro 14, 2004
Nas minhas turmas apenas cerca de 35% dos alunos acede à Internet em casa.
Dilema.
Apesar da escola possibilitar que os alunos acedam à Net, numa sala específica (Ciberteca), não é certo que a sala esteja disponível sempre que os alunos queiram e possam frequentá-la (1).
Tenho, assim, a obrigação de gerir as actividades propostas neste blogue de acordo com a realidade envolvente. Não pretendo que os pais dos alunos se sintam pressionados para mais uma despesa e entendo que é necessário sensibilizá-los para as potencialidades das novas tecnologias ao nível das aprendizagens.
Equilíbrio.
Nas minhas turmas cerca de 95% dos alunos tem o seu próprio telemóvel.
Será uma questão de prioridade!?
(1) A Ciberteca pode ser requisitada como sala de aula pelos professores, impossibilitando que outros alunos a utilizem.
Dilema.
Apesar da escola possibilitar que os alunos acedam à Net, numa sala específica (Ciberteca), não é certo que a sala esteja disponível sempre que os alunos queiram e possam frequentá-la (1).
Tenho, assim, a obrigação de gerir as actividades propostas neste blogue de acordo com a realidade envolvente. Não pretendo que os pais dos alunos se sintam pressionados para mais uma despesa e entendo que é necessário sensibilizá-los para as potencialidades das novas tecnologias ao nível das aprendizagens.
Equilíbrio.
Nas minhas turmas cerca de 95% dos alunos tem o seu próprio telemóvel.
Será uma questão de prioridade!?
(1) A Ciberteca pode ser requisitada como sala de aula pelos professores, impossibilitando que outros alunos a utilizem.
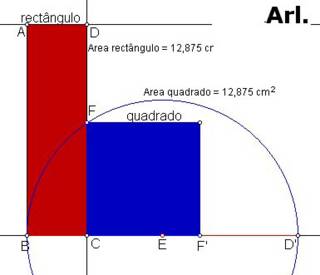
uma demonstração analítica do problema cartesiano cuja solução geométrica foi publicada anteontem
Download do Sketchpad - clica aqui-
outubro 12, 2004
outubro 10, 2004
Para os apreciadores de Música.
TREM AZUL - JAZZ STORE
R. do Alecrim, 21-A Lisboa (rua que liga o Cais do Sodré ao Lg. de Camões e ao Chiado)
Abre no próximo dia catorze.
Depois da Loja da Música, da Fnac do Colombo e da Megastore da Valentim de Carvalho esta equipa lança-se por conta própria. Trata-se de uma ousadia, certamente calculada, que merece o apoio dos amadores (no sentido camoniano) de música.
outubro 09, 2004
ÁLVARO SIZA DESENHOS
Almada - Casa da Cerca- Centro Arte Contemporânea (próximo do centro histórico e da CMA)
Entre 9 de Out. e 31 de Dez.
Porque Almada não tem apenas o fórum...
Porque os jardins da Casa da Cerca merecem a visita...
Porque desses jardins temos uma fantástica vista panorâmica do Tejo e de Lisboa...
Porque Álvaro Siza!
A entrada NÃO é paga. À borla!
Almada - Casa da Cerca- Centro Arte Contemporânea (próximo do centro histórico e da CMA)
Entre 9 de Out. e 31 de Dez.
Porque Almada não tem apenas o fórum...
Porque os jardins da Casa da Cerca merecem a visita...
Porque desses jardins temos uma fantástica vista panorâmica do Tejo e de Lisboa...
Porque Álvaro Siza!
A entrada NÃO é paga. À borla!
outubro 08, 2004
Diversidade geográfica e cultural.
Elisa vem de GOIANIA, cidade a cerca de 200km de Brasília
Radu é moldavo.
Lina é natural de STAVROPOL, cidade equidistante do Mar Negro e do Mar Cáspio, no Cáucaso.
Contei à Lina, e restantes colegas, uma histórinha verídica que se passou em Setúbal no início dos anos setenta. Nessa altura o Vitória tinha o JJ, o Duda, o Zé Maria,...o Vitor Baptista,...porém o estádio, com capacidade para trinta e cinco mil espectadores, quase nunca esgotava. Numa dessas temporadas o sorteio colocou o Vitória a disputar uma eliminatória com uma equipa de Moscovo, talvez o Spartak. Aí o estádio encheu por completo. Vierem pessoas de vários locais da região e do país para ver os russos, criaturas de terras longínquas e com fama de voraz apetite ao pequeno almoço. Era criança, mas recordo este episódio e imagino que muitos queriam ver com os próprios olhos se os russos eram gente comum ou criaturas com fios, porcas e parafusos...couraçados humanos!
Todos os alunos ficaram relativamente indiferentes e algo admirados, para eles, habituados a conviver com malta de proveniências muito diferentes, esta questão é no mínimo estranha. Eu acho curioso este reflexo de mudança e, além do mais, aprendi a dizer Geometria em russo: GUÊMÊTRÍA
Elisa vem de GOIANIA, cidade a cerca de 200km de Brasília
Radu é moldavo.
Lina é natural de STAVROPOL, cidade equidistante do Mar Negro e do Mar Cáspio, no Cáucaso.
Contei à Lina, e restantes colegas, uma histórinha verídica que se passou em Setúbal no início dos anos setenta. Nessa altura o Vitória tinha o JJ, o Duda, o Zé Maria,...o Vitor Baptista,...porém o estádio, com capacidade para trinta e cinco mil espectadores, quase nunca esgotava. Numa dessas temporadas o sorteio colocou o Vitória a disputar uma eliminatória com uma equipa de Moscovo, talvez o Spartak. Aí o estádio encheu por completo. Vierem pessoas de vários locais da região e do país para ver os russos, criaturas de terras longínquas e com fama de voraz apetite ao pequeno almoço. Era criança, mas recordo este episódio e imagino que muitos queriam ver com os próprios olhos se os russos eram gente comum ou criaturas com fios, porcas e parafusos...couraçados humanos!
Todos os alunos ficaram relativamente indiferentes e algo admirados, para eles, habituados a conviver com malta de proveniências muito diferentes, esta questão é no mínimo estranha. Eu acho curioso este reflexo de mudança e, além do mais, aprendi a dizer Geometria em russo: GUÊMÊTRÍA
outubro 07, 2004
outubro 06, 2004
Notícia do PÚBLICO - NOBEL da FÍSICA-
Quarta-feira, 06 de Outubro de 2004
Todas as coisas são feitas de átomos. E todos os átomos, no núcleo, são feitos de protões e neutrões, que por sua vez são formados por partículas ainda mais pequenas, os quarks. Tal como os quarks, uma das partículas fundamentais da natureza, pensa-se que os electrões, em redor do núcleo dos átomos, não são formados por partículas mais pequenas. Perceber o que se passa ao nível dos quarks, os constituintes mais pequenos da natureza, como fizeram os três físicos premiados com o Nobel da Física deste ano, é perceber de que são feitas as coisas. É perceber, em última análise, de que é feito o Universo, tudo o que existe.
Explicar a estrutura íntima da matéria, diz o físico Carlos Fiolhais, da Universidade de Coimbra, ajuda a perceber melhor o início do Universo e da vida. Sim, porque o homem é feito quarks, protões, neutrões, electrões, átomos, moléculas. O corpo humano é composto por algo como 10 elevado a 29 quarks: se fossem enfiados num fio, formariam um colar que daria um milhão de voltas à Terra.
Mas se não quisermos ter uma visão tão egocêntrica, no início do Universo não havia protões nem neutrões. Havia quarks, que se ligaram e deram origem aos protões e neutrões e por aí adiante. A força nuclear forte, a área do trabalho agora distinguido, teve um papel nessa união.
Três das forças fundamentais, a força nuclear forte, a força nuclear fraca e a electromagnética, aplicam-se ao mundo microscópico dos átomos. A restante força fundamental, a força gravítica, aplica-se ao mundo macroscópico, dos planetas às galáxias. Enquanto as forças forte, fraca e electromagnética estão unificadas numa teoria, a gravidade continua de fora. O trabalho dos galardoados, explicou o comunicado da Real Academia das Ciências Sueca, que atribuiu o prémio, foi mais um passo na descrição unificada de todas as forças da natureza, independentemente da escala - desde as pequeníssimas distâncias dentro do núcleo atómico às vastas distâncias do Universo. Um sonho ao qual Albert Einstein dedicou grande parte do seu tempo, sem sucesso. T.F.
Todas as coisas são feitas de átomos. E todos os átomos, no núcleo, são feitos de protões e neutrões, que por sua vez são formados por partículas ainda mais pequenas, os quarks. Tal como os quarks, uma das partículas fundamentais da natureza, pensa-se que os electrões, em redor do núcleo dos átomos, não são formados por partículas mais pequenas. Perceber o que se passa ao nível dos quarks, os constituintes mais pequenos da natureza, como fizeram os três físicos premiados com o Nobel da Física deste ano, é perceber de que são feitas as coisas. É perceber, em última análise, de que é feito o Universo, tudo o que existe.
Explicar a estrutura íntima da matéria, diz o físico Carlos Fiolhais, da Universidade de Coimbra, ajuda a perceber melhor o início do Universo e da vida. Sim, porque o homem é feito quarks, protões, neutrões, electrões, átomos, moléculas. O corpo humano é composto por algo como 10 elevado a 29 quarks: se fossem enfiados num fio, formariam um colar que daria um milhão de voltas à Terra.
Mas se não quisermos ter uma visão tão egocêntrica, no início do Universo não havia protões nem neutrões. Havia quarks, que se ligaram e deram origem aos protões e neutrões e por aí adiante. A força nuclear forte, a área do trabalho agora distinguido, teve um papel nessa união.
Três das forças fundamentais, a força nuclear forte, a força nuclear fraca e a electromagnética, aplicam-se ao mundo microscópico dos átomos. A restante força fundamental, a força gravítica, aplica-se ao mundo macroscópico, dos planetas às galáxias. Enquanto as forças forte, fraca e electromagnética estão unificadas numa teoria, a gravidade continua de fora. O trabalho dos galardoados, explicou o comunicado da Real Academia das Ciências Sueca, que atribuiu o prémio, foi mais um passo na descrição unificada de todas as forças da natureza, independentemente da escala - desde as pequeníssimas distâncias dentro do núcleo atómico às vastas distâncias do Universo. Um sonho ao qual Albert Einstein dedicou grande parte do seu tempo, sem sucesso. T.F.
outubro 05, 2004
outubro 04, 2004
outubro 03, 2004
A Escolha de Um Matemático - Público de 2/10.
O professor Nuno Crato diz que M. C. Escher "brinca com a inconsistência das projecções surpreendendo-nos com objectos impossíveis"
Há três mundos distintos nesta litografia, três perspectivas diferentes. E tudo depende do nosso olhar. Das 76 gravuras que estão no livro da Colecção Privada, o matemático Nuno Crato escolheu "Relatividade" (n.º 67), que considera "uma das mais bonitas e equilibradas e, ao mesmo tempo, das mais intrigantes" de M.C. Escher.
Que mundos são esses? "Se a olharmos na posição certa (com a assinatura do artista no canto superior esquerdo), veremos o mundo dos que andam direitos, o dos que andam deitados para a esquerda e o dos que estão deitados para a direita", explica Crato, professor do Instituto Superior de Economia e Gestão, em Lisboa. E continua: "Qualquer desses mundos é coerente e a perspectiva está perfeitamente traçada - se isolarmos um pedaço podemos considerar apenas uma das perspectivas." Escher, contudo, colocou três perspectivas diferentes na mesma gravura, "com três pontos de fuga distintos". Para Nuno Crato, é isso que torna tudo "mais interessante, pois não há apenas uma maneira de olhar para o quadro". É isso que também faz com que "diferentes mundos se interpenetrem". "Há escadas que os habitantes de mundos diversos partilham, subindo-as uns 'na vertical', outros 'deitados'", explica.
Nuno Crato diz que esta imagem é paradigmática do trabalho desenvolvido por Escher, "que explorou os paradoxos da representação no plano de um mundo que tem três dimensões". Nesse sentido, as suas "figuras impossíveis" são-no "porque projectam imagens de objectos que não poderiam existir a três dimensões se as projecções fossem lineares e consistentes". Isto porque Escher "brinca com a inconsistência dessas projecções surpreendendo-nos com objectos impossíveis". E esse é, para o professor, "um dos seus maiores fascínios enquanto artista".
É, talvez, na representação desses mundos impossíveis que Escher ("que teve como professor um judeu de origem portuguesa, Jesserum de Mesquita"), "muitas vezes sem o saber", explica Nuno Crato, criou "objectos de grande interesse matemático". Como? "Possuidor de uma grande intuição geométrica e de um grande rigor e persistência, explorou simetrias, padrões e paradoxos que põem no papel problemas matemáticos interessantes. Os matemáticos estão-lhe gratos por ter representado tão bem conceitos que agora nos são mais fáceis de explicar graças aos seus desenhos."
Nuno Crato foi a primeira pessoa em Portugal a notar que os desenhos de espirais em esferas de Escher correspondem às loxodrómias de Pedro Nunes. E, apesar de o artista não estar a par do trabalho de Nunes, Crato acredita que Escher "foi levado a redescobri-lo, desenhando". Isto porque há duas gravuras de Escher, com espirais em esferas, "em que são patentes dois pólos, meridianos e paralelos, tais como na esfera terrestre". Sobre essas esferas, continua, "desenhou curvas que as atravessam de baixo acima, fazendo ângulos constantes com os meridianos". Foi Pedro Nunes que descobriu matematicamente que "essas curvas são espirais que convergem para os pólos", explica Crato, e "correspondem, em navegação, às chamadas linhas de rumo, que os navios descrevem quando seguem uma direcção cardeal."
O professor Nuno Crato diz que M. C. Escher "brinca com a inconsistência das projecções surpreendendo-nos com objectos impossíveis"
Há três mundos distintos nesta litografia, três perspectivas diferentes. E tudo depende do nosso olhar. Das 76 gravuras que estão no livro da Colecção Privada, o matemático Nuno Crato escolheu "Relatividade" (n.º 67), que considera "uma das mais bonitas e equilibradas e, ao mesmo tempo, das mais intrigantes" de M.C. Escher.
Que mundos são esses? "Se a olharmos na posição certa (com a assinatura do artista no canto superior esquerdo), veremos o mundo dos que andam direitos, o dos que andam deitados para a esquerda e o dos que estão deitados para a direita", explica Crato, professor do Instituto Superior de Economia e Gestão, em Lisboa. E continua: "Qualquer desses mundos é coerente e a perspectiva está perfeitamente traçada - se isolarmos um pedaço podemos considerar apenas uma das perspectivas." Escher, contudo, colocou três perspectivas diferentes na mesma gravura, "com três pontos de fuga distintos". Para Nuno Crato, é isso que torna tudo "mais interessante, pois não há apenas uma maneira de olhar para o quadro". É isso que também faz com que "diferentes mundos se interpenetrem". "Há escadas que os habitantes de mundos diversos partilham, subindo-as uns 'na vertical', outros 'deitados'", explica.
Nuno Crato diz que esta imagem é paradigmática do trabalho desenvolvido por Escher, "que explorou os paradoxos da representação no plano de um mundo que tem três dimensões". Nesse sentido, as suas "figuras impossíveis" são-no "porque projectam imagens de objectos que não poderiam existir a três dimensões se as projecções fossem lineares e consistentes". Isto porque Escher "brinca com a inconsistência dessas projecções surpreendendo-nos com objectos impossíveis". E esse é, para o professor, "um dos seus maiores fascínios enquanto artista".
É, talvez, na representação desses mundos impossíveis que Escher ("que teve como professor um judeu de origem portuguesa, Jesserum de Mesquita"), "muitas vezes sem o saber", explica Nuno Crato, criou "objectos de grande interesse matemático". Como? "Possuidor de uma grande intuição geométrica e de um grande rigor e persistência, explorou simetrias, padrões e paradoxos que põem no papel problemas matemáticos interessantes. Os matemáticos estão-lhe gratos por ter representado tão bem conceitos que agora nos são mais fáceis de explicar graças aos seus desenhos."
Nuno Crato foi a primeira pessoa em Portugal a notar que os desenhos de espirais em esferas de Escher correspondem às loxodrómias de Pedro Nunes. E, apesar de o artista não estar a par do trabalho de Nunes, Crato acredita que Escher "foi levado a redescobri-lo, desenhando". Isto porque há duas gravuras de Escher, com espirais em esferas, "em que são patentes dois pólos, meridianos e paralelos, tais como na esfera terrestre". Sobre essas esferas, continua, "desenhou curvas que as atravessam de baixo acima, fazendo ângulos constantes com os meridianos". Foi Pedro Nunes que descobriu matematicamente que "essas curvas são espirais que convergem para os pólos", explica Crato, e "correspondem, em navegação, às chamadas linhas de rumo, que os navios descrevem quando seguem uma direcção cardeal."
outubro 02, 2004
Subscrever:
Comentários (Atom)