janeiro 28, 2007
janeiro 23, 2007
janeiro 17, 2007
janeiro 15, 2007
Encontrei o Palma!
Já é Engenheiro. Tal como o Esteves.
Licenciados pelo Instituto Superior Técnico.
O Luís concluiu uma licenciatura no ISCTE e a sua irmã gémea é Nutricionista.
A Rita licenciou-se em Farmácia e, neste momento, está a fazer o estágio numa farmácia de Setúbal.
Foram alunos na nossa escola. Fizeram parte da primeira geração de alunos aos quais foi permitida a utilização de calculadora gráfica em exames nacionais (Junho de 2000) . A calculadora gráfica e o viewscreen constituíram materiais didácticos utilizados com regularidade nesse triénio. Os profetas e arautos do desastre do ensino da Matemática terão em linha de conta o percurso destes alunos? Ou será que o desastre do ensino da Matemática é extensível ao Departamento de Matemática do IST? Alunos que passaram pelo Buescu, pelo Sousa Ramos, pelo Paulo Almeida e outros insuspeitos…
O desastre é, definitivamente, de outra natureza!
Já é Engenheiro. Tal como o Esteves.
Licenciados pelo Instituto Superior Técnico.
O Luís concluiu uma licenciatura no ISCTE e a sua irmã gémea é Nutricionista.
A Rita licenciou-se em Farmácia e, neste momento, está a fazer o estágio numa farmácia de Setúbal.
Foram alunos na nossa escola. Fizeram parte da primeira geração de alunos aos quais foi permitida a utilização de calculadora gráfica em exames nacionais (Junho de 2000) . A calculadora gráfica e o viewscreen constituíram materiais didácticos utilizados com regularidade nesse triénio. Os profetas e arautos do desastre do ensino da Matemática terão em linha de conta o percurso destes alunos? Ou será que o desastre do ensino da Matemática é extensível ao Departamento de Matemática do IST? Alunos que passaram pelo Buescu, pelo Sousa Ramos, pelo Paulo Almeida e outros insuspeitos…
O desastre é, definitivamente, de outra natureza!
janeiro 12, 2007
Ao entrar no site ludicum.org com a intenção de procurar informações sobre os CNJM, deparei com o nome José Sousa Ramos. Prioridades invertidas, segui para o link com o seu nome. Desde 1997 ou 98 que seguia com interesse as suas ideias, expressas no seu WebSite, sobre o ensino e a aprendizagem da Matemática. Ideias vanguardistas, não necessariamente consensuais mas loucas e utópicas, prenhes da paixão pelo ser humano e pela Matemática. Ideias que precisam de um mundo melhor para se tornarem exequíveis. Ideias que exigem que se subam patamares ao nível da mentalidade vigente. Ideias que, num outro sentido, podem, elas próprias constituir um valioso contributo para a nossa evolução colectiva.
Quando tive conhecimento que o Prof. Sousa Ramos iria dar uma aula/palestra no ProfMat de Portimão, em 1999, a minha agenda ficou condicionada e não me arrependi. A sala encheu-se para ouvir a sua dissertação apaixonada e livre. A palestra, Da complexidade da Natureza à complexidade da Matemática, foi extremamente interessante.
Quando tive conhecimento que o Prof. Sousa Ramos iria dar uma aula/palestra no ProfMat de Portimão, em 1999, a minha agenda ficou condicionada e não me arrependi. A sala encheu-se para ouvir a sua dissertação apaixonada e livre. A palestra, Da complexidade da Natureza à complexidade da Matemática, foi extremamente interessante.
Ao entrar no site ludicum.org dei-me conta do falecimento prematuro do Professor José Sousa Ramos. Li o tributo que lhe prestou o Prof. Paulo Almeida e o testemunho comovente de um seu ex-aluno. Não deixem de os ler!

Prof. José de Sousa Ramos (1948-2007)
janeiro 09, 2007
janeiro 08, 2007
Número de Ouro (cont.) O triângulo [ABC] é isósceles, sendo 72º a amplitude do ângulo interno cujo vértice é o ponto A. Partindo deste triângulo, constrói-se um segundo triângulo [ABD], sabendo que a medida do comprimento dos segmentos [AB] e [AD] é igual. A razão entre as áreas dos dois triângulos é igual ao número de ouro.
O triângulo [ABC] é isósceles, sendo 72º a amplitude do ângulo interno cujo vértice é o ponto A. Partindo deste triângulo, constrói-se um segundo triângulo [ABD], sabendo que a medida do comprimento dos segmentos [AB] e [AD] é igual. A razão entre as áreas dos dois triângulos é igual ao número de ouro.
 O triângulo [ABC] é isósceles, sendo 72º a amplitude do ângulo interno cujo vértice é o ponto A. Partindo deste triângulo, constrói-se um segundo triângulo [ABD], sabendo que a medida do comprimento dos segmentos [AB] e [AD] é igual. A razão entre as áreas dos dois triângulos é igual ao número de ouro.
O triângulo [ABC] é isósceles, sendo 72º a amplitude do ângulo interno cujo vértice é o ponto A. Partindo deste triângulo, constrói-se um segundo triângulo [ABD], sabendo que a medida do comprimento dos segmentos [AB] e [AD] é igual. A razão entre as áreas dos dois triângulos é igual ao número de ouro. janeiro 07, 2007
Número de ouro (cont.)
Um rectângulo cuja razão entre o comprimento e a largura é igual ao número de ouro, ou seja, aproximadamente 1,618 era considerado estéticamente perfeito para os para os Gregos (antiguidade clássica). Supõe-se que esta regra foi utilizada pelo escultor Phidias no projecto da fachada do templo Parténon, na Acróplole de Atenas.
Um rectângulo cuja razão entre o comprimento e a largura é igual ao número de ouro, ou seja, aproximadamente 1,618 era considerado estéticamente perfeito para os para os Gregos (antiguidade clássica). Supõe-se que esta regra foi utilizada pelo escultor Phidias no projecto da fachada do templo Parténon, na Acróplole de Atenas.

Nas figuras em baixo, estão representados dois rectângulos de ouro construídos no Sketchpad. A construção de um rectângulo com esta característica é muito fácil de fazer com lápis e compasso. Partindo de um quadrado (na figura a amarelo) ...
1. ...acha-se o ponto médio M de [AD]...
2. ...esboça-se o segmento cujos extremos são os pontos M e C...
3. ...coloca-se a ponta seca do compasso no ponto M, abre-se o mesmo até ao ponto C e efectua-se a rotação deste ponto. Da intersecção do arco de circunferência com a recta AD resulta o ponto F...
4. ...
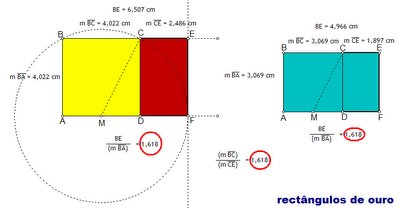
Experimenta! Desenha um quadrado qualquer, constrói um rectângulo de ouro, efectua as medições do lado do rectângulo obtido e do lado do quadrado original...
janeiro 05, 2007

Em qualquer pentágono regular a razão entre a medida da diagonal e a medida do lado é um valor constante: 1,618(no exemplo apresentado). Este é uma valor aproximado do número de OURO!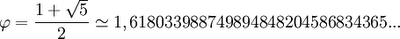
Subscrever:
Comentários (Atom)