Número de ouro (cont.)
Um rectângulo cuja razão entre o comprimento e a largura é igual ao número de ouro, ou seja, aproximadamente 1,618 era considerado estéticamente perfeito para os para os Gregos (antiguidade clássica). Supõe-se que esta regra foi utilizada pelo escultor Phidias no projecto da fachada do templo Parténon, na Acróplole de Atenas.

Nas figuras em baixo, estão representados dois rectângulos de ouro construídos no Sketchpad. A construção de um rectângulo com esta característica é muito fácil de fazer com lápis e compasso. Partindo de um quadrado (na figura a amarelo) ...

1. ...acha-se o ponto médio M de [AD]...

2. ...esboça-se o segmento cujos extremos são os pontos M e C...

3. ...coloca-se a ponta seca do compasso no ponto M, abre-se o mesmo até ao ponto C e efectua-se a rotação deste ponto. Da intersecção do arco de circunferência com a recta AD resulta o ponto F...

4. ...

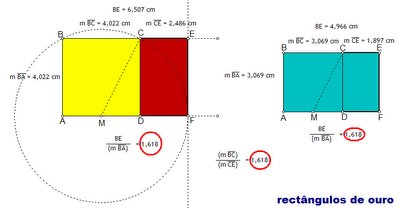
Experimenta! Desenha um quadrado qualquer, constrói um rectângulo de ouro, efectua as medições do lado do rectângulo obtido e do lado do quadrado original...